What is Boundary Representation (B-Rep)?
Koji Takaba • B-Rep, or boundary representation, is a term you will likely come across during any research involving 3D modeling. It is the most popular method used to represent 3D shapes in a computer. Understanding the basics of how B-Rep is useful for those considering developing their own applications that leverage 3D technology, those who use the tools themselves, or anyone involved in industries that do.
How To Represent 3D Objects on a Computer
While modern software allows us to circumvent it most of the time, everything put into a computer boils down to math.
When representing 3D shapes in a computer, you need to break them down into equations that define entities in a 3D space. For a shape like a sphere, this is easy: a single equation can define the entire structure. For others, the process is significantly more complex.
A good starting shape to learn from is a cylinder. No one equation can fully define the shape: they would leave the height of the cylinder as infinite. To prevent this, we need to establish a boundary for the top and bottom face of the shape. This gives the height of the cylinder its definition but leaves the top and bottom faces out. B-Rep works by defining the limitations of an entity’s volume, so we need to cap both ends of the cylinder.
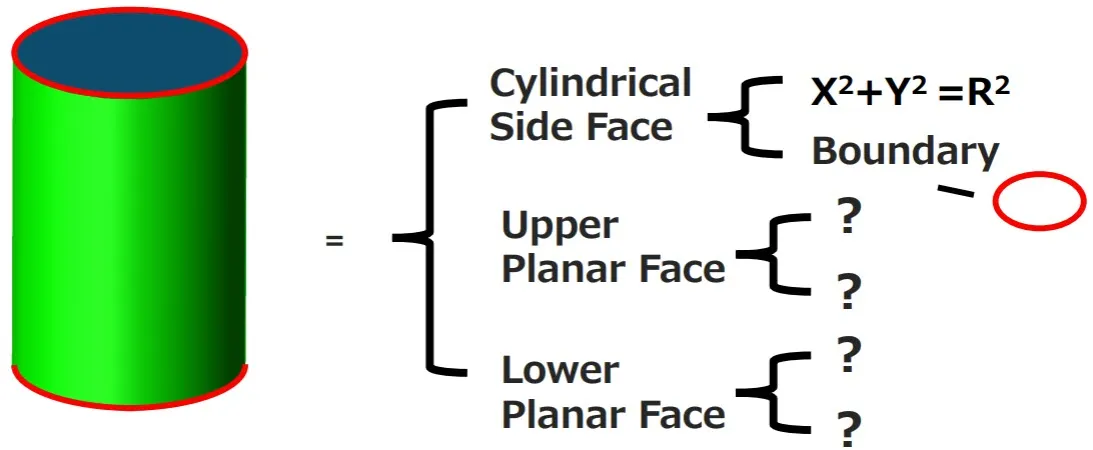
To do this, we will divide it into three components: the cylindrical side face (defined by the simple equation and boundary), the upper planar surface, and the lower planar surface. The next problem to solve is representing the two planar surfaces.
A plane is infinite by default, so much like the cylindrical side face, we have to set boundaries to represent the shape correctly. For our cylinder, they are exactly the same boundaries we used for the cylindrical side face.
The cylinder has three faces, each with its own equation and boundary. In B-Rep theory, we call the equations “geometry” and the faces/boundaries the “topology”.
How To Represent a Cube in a Computer
Just like a cylinder, a cube cannot be defined in 3D space by a single equation. We must once again break it down into its faces and boundaries. The equation (or geometry) for each face is simple enough, but the boundaries represent a challenge. The boundaries are four straight lines, and like the planes before, lines without definition are infinite. In a computer, we define a start and end point of the lines to solve this.
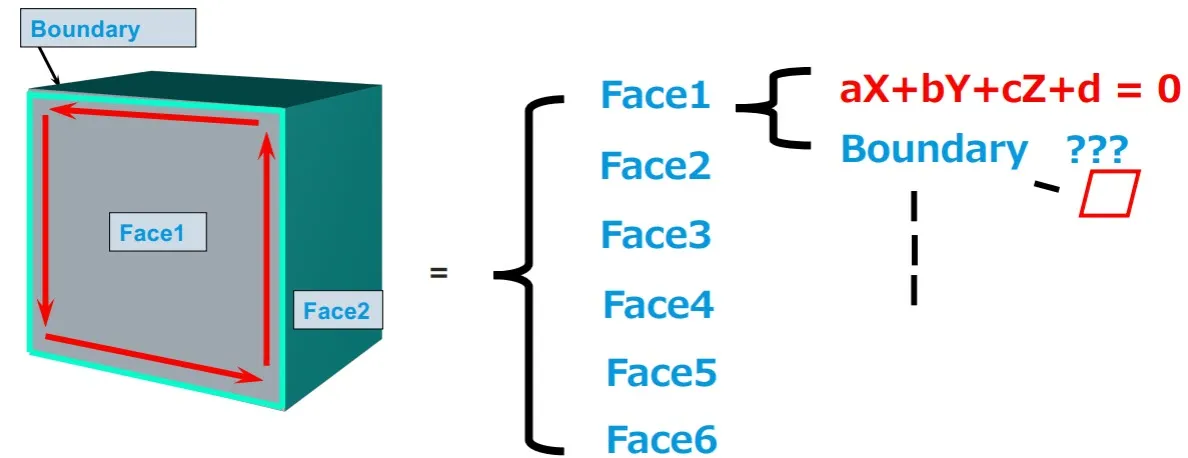
To continue discussing our cube, we will use some terms used in Siemens Parasolid, the leading 3D geometric kernel of which Tech Soft 3D is a proud reseller.
B-Rep in Parasolid
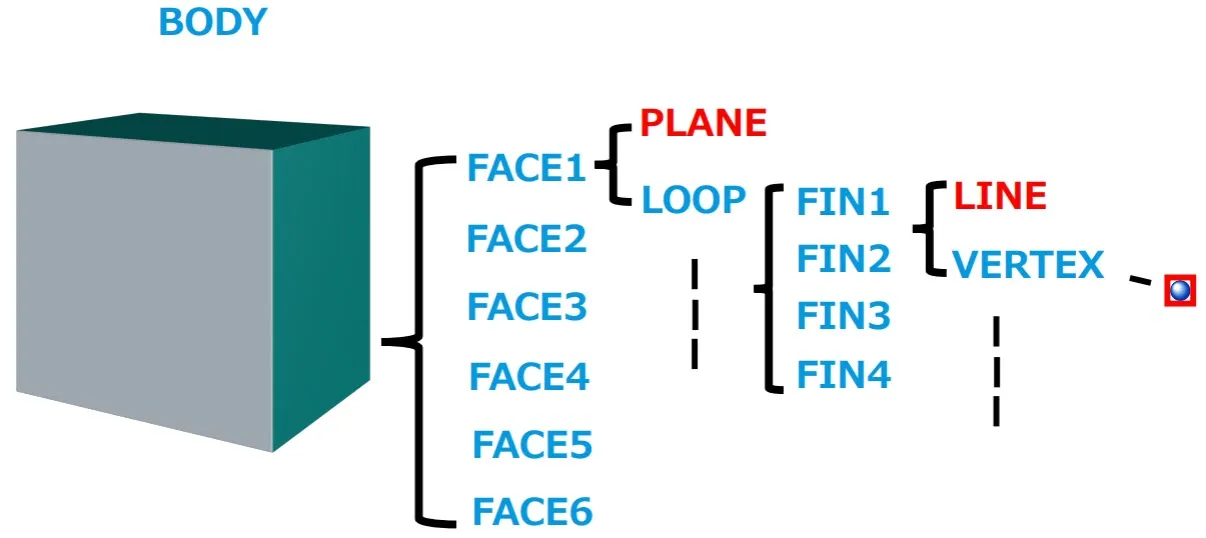
In Parasolid, a straight line is expressed as an edge or a fin. An edge represents the topology of a curve, and it is independent from other lines. A fin serves as one part of a loop.
On our cube, we have 6 faces, each of which connects to a plane geometry and loop topology. Each loop consists of four fins, and each fin is made up of a line and vertex (end point).
In B-Rep, hierarchy is crucial for both functional software and to help understand how the process works. Seeing how each element of the modeling kernel is made up of other entities, you can better understand how we turn math into a 3D representation of an object. B-Rep is able to represent any 3D shape through its geometry and topology.
If you're involved in the CAD world as a developer, user, decision-maker, student, or any other role, you'll want to stay up-to-date on the latest CAD trends. Check out our piece on the "5 CAD Trends to Watch For in 2024 and Beyond".
Got a question? Let one of our experts help you find the
answer